Math and Statistics Tutoring by a Top Expert

The tesseract helps mathematicians and physicists conceptualize and study properties of higher-dimensional spaces, which are not easy to visualize. For example, models in string theory often require multiple dimensions beyond the familiar 3 dimensions. It is constructed by connecting corresponding vertices of two cubes in four-dimensional space, resulting in 16 vertices, 32 edges, 24 square faces, and 8 cubic cells.

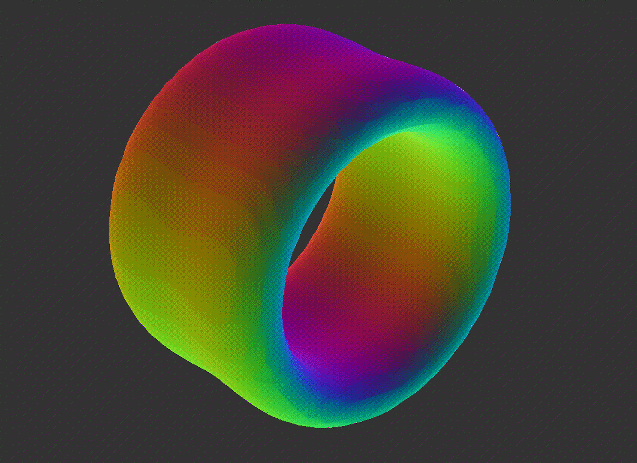
In topology, a cylinder and a donut (torus) are not the same, but they are often considered similar in the sense that they both have a single hole or handle. This similarity is explored through the concept of topological equivalence or homeomorphism, which focuses on properties that remain unchanged under continuous deformations like stretching or bending.

A polyhedron with pentagonal faces is called a dodecahedron. Specifically, the regular dodecahedron is one of the five Platonic solids and consists of 12 pentagonal faces, 20 vertices, and 30 edges. All of its faces are regular pentagons, and the angles between them are identical, making it a highly symmetrical shape. There are also other polyhedra, like certain Goldberg polyhedra or Archimedean solids, that may have some pentagonal faces mixed with other polygonal faces.

In topology, a point and a torus are not directly equivalent, but they can be related through continuous transformations or specific topological processes. Contractibility: - A point is considered a contractible space, which means it can be continuously shrunk to itself without any tearing or cutting.

Just an optical illusion.